
satisfies condition (i) of my last answer. Every infinitely many times differentiable function is obviously continuously differentiable, i.e. This means that the discussion is over, since you could not agree with two obvious facts extracted from the discussion for getting at least something what we commonly can agree. Differentiability on an open set implies that derivatives of arbitrary order exist. You can have real functions that are once continuously differentiable but whose second derivative does not exist anywhere.

Differentiability for real functions is a much less restrictive property than for complex ones. This again shows that it may not be a good idea in this case to consider complex functions when one is searching for an answer to a question on real functions only. The branch points will get replaced by essential singularities which are much weaker singularities along the real axis but much more ferocious off it. This does not mean that all its singularities go away. In fact, it is possible to get it infinitely often differentiable by appropriate deformation near the junction points.

These branch points can be removed by making the function smoother at the joints. Now regarding the second function, which when taken as the real part of a complex function and thus extended to the complex plane (it must have a non-vanishing imaginary part on the real axis, because the real part alone is not analytic) will indeed develop branch points at the junction points of the piecewise definition. So your "definition" is not useful on infinite intervals either.) (On infinite intervals, bounded variation does not guarantee integrability, a constant different from zero has zero variation, but is not integrable on the infinite interval. Therefore, the definition of bounded variation has to deal with functions that are not necessarily (piecewise) differentiable. For a continuous or differentiable function, the answer is immediate - it is always of bounded variation on a closed interval. But the concept of bounded variation was introduced to discuss integrability of functions on closed (or at least finite) intervals. If your function is piecewise differentiable, you may use that formula to do the calculation. This was not to mean that it is wrong to calculate the variation from the integral of |f'(x)|, it was only to indicate that this integral is not a useful definition of the total variation (and I don't think it is used as a definition in the books you indicate). You said in an earlier post: "If one considers the total variation of a function over an interval as being equal to the integral of the absolute value of the derivative of that function over that interval (which is the standard definition of total variation for differentiable functions in every respectable text - it is used by Hardy and Littlewood, by Daniell, and by Von Neumann, to name but three authorities*)," and I answered with a reference to the definition of the notion of bounded variation on Wikipedia. Because infinity is not a number, there is no point in asking what number is more than infinity.Anyway, to explain a bit more my last post. A number can approach infinity, that is to say, get larger and larger and larger, but it will never get there.
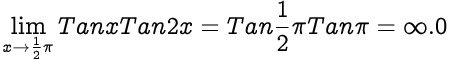
(If you started counting really fast for billions of years, you would never get to infinity.) There are, however, different "sizes of infinity." Aleph-null, for example, is the infinity that describes the size of the natural numbers (0,1,2,3,4.) The infinity that describes the size of the real numbers is much larger than aleph-null, for between any two natural numbers, there are infinite real numbers.Anyway, to improve upon the answer above, it is not meaningful to say "when x is infinity," because, as explained above, no number can "be" infinity. Whereas a number represents a specific quantity, infinity does not define given quantity. This does not mean that 2x when x is infinity is twice infinity, it just means that, right before x becomes infinity, the ratio is right before 2.Infinity should not be thought of as a number, but rather as a direction. That value is indeterminate, because infinity divided by infinity is defined as indeterminate, and 2 times infinity is still infinity.But, if you look at the limit of 2x divided by x, as x approaches infinity, you do get a value, and that value is 2. Take, for example, 2x divided by x, when x is infinity. Infinity is defined to be greater than any number, so there can not be two numbers, both infinity, that are different.However, when dealing with limits, one can approach a non-infinite value for a function involving infinity. There is no number greater than infinity.


 0 kommentar(er)
0 kommentar(er)
